

Introduction
About me
Associate professor at the Department of Logic,
College of Arts ("Faculty of Arts"), Charles University in PragueFilozofická fakulta UK,
Palachovo nám. 2, 11638 Praha 1.
Courses Computability (an introduction to recursive functions),
Classical Logic II (with an emphasis on incompleteness and undecidability),
and some others related to metamathematics or to algorithms.
Research interests
Interpretability of axiomatic theories, arithmetization, related modal logics, algorithmic aspects
of non-classical logics.
Experience and education
During 1982-90 worked as a software developer for an industrial company ČKD Polovodiče.
Participation in writing a control system for PDP-11 computers.
The system was designed by Jan Pavelka*)Accidentally
the same Jan Pavelka who, a few years before turning into a respected software developer,
wrote innovative papers about fuzzy logics., and was successfully applied in
several branches of industry like steel rolling or international transport of natural gas.
Ph.D. in mathematical logic, Ph.D. study in the Institute of Mathematics of the Academy of Sciences
of the Czech Republic.
Dissertation Self-Reference and Modal Logic, 1982,
supervisor Petr Hájek. Graduated in mathematics from Charles University, 1978,
master's thesis Degrees of Interpretability.
Office info, events, miscellaneous updates
Office hours Thu 15:00, or by appointment.
For more info please see the image above, or the web of the
department.
Nabídka témat bakalářských a diplomových prací:
TemataPraci13.pdf
Publications
BibTeX file
BibTeX entries can be taken from sv.bib. Note that the file
contains a preamble with some strings and macros.
Book
- Logika: neúplnost, složitost a nutnost
(Logic: Incompleteness, Complexity, and Necessity),
Academia Praha, 2002.
464 pages,
section 5.2 about Gödel-Dummett fuzzy logic was written by Petr Hájek. See the
"Book" tab above.
Some workshop or conference presentations
-
Logika, Gödel, neúplnost (Logic, Gödel, Incompleteness).
A talk at Friday meetings of Sysifos,
February 23th, 2018. A videorecord created by Ludvík Hájek is available on
YouTube.
-
Kurt Gödel: úplnost a neúplnost (Kurt Gödel: Completeness and
Incompleteness). A talk at Hvězdárna and planetárium Brno (Brno Observatory and Planetarium),
March 9th, 2017. A videorecord created by Josef Forman is available on
YouTube.
-
Rosser Sentences and Rosser Logics.
A talk at the Prague gathering of logicians,
Jan 2017.
-
On Purely implicational Fragments of Intuitionistic
Propositional Logic. A talk at the Logica '11 International Conference,
Hejnice, Czech Republic, June 2011. [pdf4]
Papers
- Do We Need Recursion? In I. Sedlár and M. Blicha, eds.,
The Logica Yearbook 2019,
pp. 193–204. College Publications, London, 2020. [pdf][talk]
- Modern Czech Logic:
Vopěnka and Hájek, History and Background. Journal of Applied Logics — IfCoLoG Journal
of Logics and their Applications, 5(6):1261–1271, 2018. [pdf]
- Předmluva: o logice 20. století (Preface: On the 20th Century Logic).
In L. Dostálová, ed., Kurt Gödel: úplnost a neúplnost (Kurt Gödel: Completeness and Incompleteness),
pp. 13–53. OPS in collaboration with University of West Bohemia Publishing,
Plzeň, 2015. ISBN 978-80-87269-39-8. In Czech. [pdf]
- On Strong Fragments of Peano Arithmetic.
In P. Arazim and M. Dančák, eds.,
The Logica Yearbook 2014,
pp. 281–291. College Publications, London, 2015. [pdf][talk]
- Výuka logiky bez logických pojmů (Teaching logic without the use
of logical notions). In L. Dostálová and K. Šebela, eds.,
Organon VII — Nihil novi, pp. 49–57. University of West Bohemia Publishing,
Plzeň, 2011. ISBN 978-80-261-0035-5. In Czech.
[pdf][pdf2]
- Infinite natural numbers: an unwanted phenomenon, or a useful concept?
In M. Peliš and V. Punčochář, eds.,
The Logica Yearbook 2010,
pp. 283–294. College Publications, London, 2011. [pdf][pdf2][talk]
- Decision Problems of Some Intermediate Logics and Their Fragments. In M. Peliš, ed.,
The Logica Yearbook 2009,
pp. 297–307. College Publications, London, 2010. [pdf][pdf2][talk]
- Relatives of Robinson Arithmetic. In M. Peliš, ed.,
The Logica Yearbook 2008,
pp. 253–263. College Publications, London, 2009. [pdf][pdf2][talk]
-
On Interpretability in the Theory of Concatenation.
Notre Dame Journal of Formal Logic, 50(1):87–95, 2009.
[pdf][pdf2]
- Weak Theories and Essential Incompleteness. In M. Peliš, ed.,
The Logica Yearbook 2007, pp. 213–224. Filosofia, Praha, 2008.
[pdf][pdf2][talk]
-
An Interpretation of Robinson Arithmetic in its Grzegorczyk's Weaker Variant.
Fundamenta Informaticae, 81(1–3):347–354, 2007.
[pdf][pdf2]
- Gödel-Dummett Predicate Logics and Axioms of Prenexability.
In O. Tomala and R. Honzík, eds.,
The Logica Yearbook 2006, pp. 251–260. Filosofia, Praha, 2007.
[pdf][pdf2][talk]
- On Modal Systems with Rosser Modalities. In M. Bílková and O. Tomala, eds.,
The Logica Yearbook 2005, pp. 203–214. Filosofia, Praha, 2006.
[pdf][pdf2][talk]
-
On Sequent Calculi for
Intuitionistic Propositional Logic.
Comm. Math. Univ. Carolinae, 47(1):159–173, 2006.
[pdf][pdf2]
-
With Blanka Kozlíkova, On
Interplay of Quantifiers in Gödel-Dummett Fuzzy Logics.
Archive for Math. Logic, 45(5):569–580, 2006.
[pdf][pdf2]
-
Note on
Inter-Expressibility of Logical Connectives in Finitely-Valued Gödel-Dummett Logics.
Soft
Computing, 10(7):629–630, 2006.
[pdf][pdf2]
-
Gödlov prvi izrek o nepolnosti.
Obzornik za matematiko in fyziko, 51(4):113–121, 2004.
-
The limit lemma
in fragments of arithmetic. Comm.
Math. Univ. Carolinae, 44(3):565–568, 2003.
[pdf][pdf2]
-
A
note on arithmetical completeness of theories with Rosser modalities.
In K. Bendová and P. Jirků, eds., Miscellanea logica V,
pp. 123–132. Karolinum, Praha, 2003. ISBN 80-246-0799-9.
-
On
structural proofs of Gödel First Incompleteness Theorem.
In K. Bendová and P. Jirků, eds., Miscellanea logica V,
pp. 115–122. Karolinum, Praha, 2003. ISBN 80-246-0799-9.
-
The decision problem of
provability logic with only one atom.
Archive for Math. Logic, 42(8):763–768, 2003.
Errata: The final paragraph, just before the list of references, contains an unpleasant
misprint: 'added in January 2002', should be 'added in January 2003'. My apologies!
[pdf][pdf2]
-
On the polynomial-space
completeness of intuitionistic propositional logic.
Archive for Math. Logic, 42(7):711–716, 2003.
[pdf][pdf2]
-
With K. Bendová,
On Inter-Expressibility
of Logical Connectives in Gödel Fuzzy Logic.
Soft
Computing, 4(2):103–105, 2000.
[pdf][pdf2]
-
On Provability Logic.
Nordic
Journal of Philosophical Logic, 4(2):95–116, 2000.
[pdf][pdf2]
-
Arithmetical
Classification of the Set of All Provably Recursive Functions.
Comm. Math. Univ. Carolinae, 40(4):631–634, 1999.
[pdf][pdf2]
-
Poznamka
o vztahu vyplyvani v klasicke predikatove logice (A Note on
the Consequence Relation in Classical Predicate Logic). In
P. Jirků and V. Švejdar, eds., Miscellanea
Logica II. Karolinum, Praha, 1999. In Czech.
-
Logika
v aritmetice. In P. Jirků and V. Švejdar, eds.,
Miscellanea Logica I. Karolinum, Praha, 1998. In Czech.
-
With P. Hájek, Matematicka logika (Mathematical Logic).
Praha, November 1994. Lecture notes, electronic version only, in Czech.
-
Some Independence Results in Interpretability Logic.
Studia Logica, 50(1):29–38, 1991.
- With P. Hájek,
A Note on the Normal Form of Closed Formulas
of Interpretability Logic. Studia Logica, 50(1):25–28, 1991.
-
Modal Analysis of Generalized Rosser Sentences. J. Symb. Logic, 48(4):986–999, 1983.
[JSTOR]
-
A Sentence that is Difficult to Interpret.
Comm. Math. Univ. Carolinae,
22(4):661–666, 1981.
-
Degrees of Interpretability.
Comm. Math. Univ. Carolinae,
19(4):789–813, 1978.
Logic: Incompleteness, Complexity, and Necessity (Academia, 2002)
I do not think logic is a field where people are taught how to think logically.
Instead, I consider it a theory about deductive thinking for people who already
are able to think logically, usually because they have some experience with
academic mathematics.
My ambition was to have more than a list of definitions, theorems, and proofs; I am
trying to include comments and explanations, and I believe that the reader should be led
from some questions to some solutions.
I am grateful to Petr Hájek, who was my teacher and who gave one of the initial
impulses for writing this book. He actually wrote only a small part of the text, but
much larger part and perhaps everything was inspired by him.
As a result of an agreement with the Academia publishing company,
a pdf version of the book is now available
(full text!) for study purposes (only!). When downloading the file, it is recommended
to download also Errata
and save both files to the same folder on local computer. That will activate the links
in the text marked by big red 'E'.
Redistribution and modifications of the file are not allowed! Printing of
(any part of) the document is not allowed!
Po domluvě s nakladatelstvím Academia je nyní
plný text knihy ve formátu pdf
přístupný pro studium (pouze!). Při kopírování souboru na lokální
počítač je doporučeno stáhnout také Errata
a umístit oba soubory do téže složky. Soubor nesmí být dále šířen
ani nesmí být modifikován! Žádná jeho část nesmí být tištěna!
Click on the blue word 'Academia' on the first page of the book to obtain
further information about their bookstores and other books they publish.
Comments and additions to Errata are welcome.
Modal and non-classical logics
Exams
Please solve at least 11 exercises from the recently updated list
and bring a list of them (just their numbers) to the exam. The ability to distinguish intuitionistic tautologies
and non-tautologies is considered a must no matter whether the corresponding exercise (number 12) is on
your list.
Course contents in Fall 2024/25
- Jan 9th, 2025
- Intuitionistic tautologies and non-tautologies, constructions of Kripke counterexamples.
The Rieger-Nishimura lattice of infinitely many intuitionistically non-equivalent formulas built up from
a single atom. This was left without a proof. The relationship between classical and intuitionistic logic:
Glivenko's (not, as mistakenly stated in the lecture, Kolmogorov's) theorem says that A is
a classical tautology if and only if ¬¬A is an intuitionistic tautology. This theorem
is described as an embedding of classical logic into intuitionistic logic, and it actually says
that of the two, intuitionistic logic is the richer. The sequent calculus GJ. Saturated sequents. The completeness
proof for GJ remained unfinished, but it can be reconstructed by modifying a completeness proof for K4
given in the exercises.
- Dec 19th, 2024
- Kripke semantics of intuitionistic propositional logic. Every intuitionistic tautology is a classical
tautology, but not vice versa.
Homework 1. Verify that
A∨¬A → (¬¬A → A)
is an intuitionistically tautological schema.
Homework 2. Is
(¬C → A∨B) → (¬C→A) ∨ (¬C→B) an intuitionistically tautological schema?
- Dec 12th, 2024
- Bisimulation between frames or models. The characteristic class of a logic is closed under p‑morphic images,
disjoint unions and subframes generated by a node. This fact yields a tool for proving that a particular class
(like the class of all irreflexive frames) is not the characteristic class of any logic.
Homework 1. Prove that the class of all asymmetric frames (where the accessibility relation
satisfies ∀x∀y(xRy ⇒ ¬(yRx))
is not the characteristic class of any logic.
Homework 2. Find the characteristic class of the
schema □(□A → B) ∨ □(□B → A).
Write down a justification of your answer.
Homework 3. Determine whether the class of all 〈W,R〉 where R
is a strict linear order on W is the characteristic class of some logic.
- Dec 5th, 2024
- Cresswell's model showing that K + H ⊬ L. Sequent calculus for GL
has a single modal rule 〈Γ,□Γ,□A ⇒ A〉 / 〈□Γ ⇒ □A〉. The decision procedure (proof of the completeness theorem)
for K can be modified so that it works for GL.
Homework 1. Consider the Cresswell's frame and the valuation where p is refuted at a0
and satisfied at all other nodes, and other atoms are everywhere refuted. Identify the nodes that refute the
formula □(□p → p) → □p.
Find an instance of L that is refuted at a2.
Homework 2. Prove the formula ¬□⊥ → ¬□¬□⊥
in the sequent calculus for GL.
- Nov 28th, 2024
- The closure of K under the un-necessitation rule can also be proved proof-theoretically.
The characteristic class of the schema L is the class of all transitive reversely well-founded frames.
The same class is (somewhat surprisingly) the characteristic class of the schema H, and thus
the question whether K + H ⊢ L is not answered yet.
Homework. A sequent calculus for K4 has only one modal rule 〈Γ,□Γ ⇒ A〉 / 〈□Γ ⇒ □A〉. Prove that if a
formula A is provable in the Hilbert-style calculus for K4, then the
sequent 〈 ⇒ A〉 is provable in the sequent calculus for K4.
Also prove that if 〈Γ ⇒ Δ〉 is provable in the
sequent calculus, then the implication ⋀Γ → ⋁Δ
is provable in the Hilbert-style calculus. Write only the steps that you find essential and skip the
routine (or known) ones.
- Nov 21st, 2024
- Euclidean relations. The notion of characteristic class. Characteristic classes of the traditional
modal logics and schemas.
Homework. Use characteristic classes (that is, avoid speaking about truth valuations) and prove
that K4 + 5 ⊬ B. Also show
that T + B ⊬ 5.
- Nov 14th, 2024
- A strong variant of completeness theorem for K: every sequent has a cut-free proof or a finite cycle-free
counterexample. Thus the cut-elimination theorem and finite model property hold for K. One of several consequences
is the following. The set of all formulas provable in K is closed under the rule LR: if
□A → A is provable in K, then also A is
provable. Thus adding LR to K yields no new provable formulas.
Homework. Invent a brief semantic argument (a picture and a comment in one or two lines) showing that
the set of all formulas provable in K is closed under the un-necessitation rule: if □A
is provable in K, then also A is provable.
- Nov 7th, 2024
- First of several soundness theorems: K is sound w.r.t. the class of all Kripke models, T and K4 are
sound w.r.t. the class of all models whose accessibility relation is reflexive (or transitive, respectively).
An algorithm (processing sequents) about which it is clear that it terminates on every input.
Next week we will deduce some theorems, completeness of K included, from this algorithm.
Homework 1. Find a Kripke model K = 〈W,R,⊩〉
and a formula A such that □A → A
is but A is not valid in K. Can the model K be chosen so that it is
irreflexive, i.e. such that no node in it is accessible from itself?
Homework 2. Characterize (describe in words) all Kripke models in which the
formula ¬□⊥ → ¬□¬□⊥ is valid.
Construct a model demonstrating that
□(□p → p) → □p is
not provable in K4 plus ¬□⊥ → ¬□¬□⊥.
Again, can the model be chosen so that it is irreflexive?
- Oct 31st, 2024
- Equivalent axiomatizations of GL: K4 plus L, or K plus L, or K4 plus LR,
or K4 plus H. Problems
to be solved: can L (or the schema 4) be proved in K plus LR? Can L (or the schema 4) be proved
in K plus H? Kripke semantics of modal logic: frames, models and forcing relations (written as ⊩).
Homework 1. Consider a model having four nodes 1, 2, 3 and 4 such that
the nodes 3 and 4 are accessible from 1, the node 1 is accessible from 2, and
the nodes 2 and 4 are accessible from 4.
The atom p is satisfied at 1 and 2.
Identify the nodes at which the formula ◇□◇p is satisfied.
Homework 2. Consider a model having three nodes 1, 2 and 3 where 1 sees 2
and both 2 and 3 see 3. Let p be satisfied at 2 and 3 and
refuted at 1, and let all other atoms be everywhere refuted. Prove (write down a full proof consisting of Czech
or English sentences) that every modal formula A
is satisfied at 2 if and only if it is satisfied at 3. Conclude that all instances of
the schema 4 are satisfied at all three nodes of this model.
- Oct 24th, 2024
- Arithmetic semantics of modal logic: necessity is understood as provability formalized inside Peano
arithmetic PA. The set ArTaut of all modal formulas that are arithmetic tautologies contains all
propositional tautologies and all instances of the schemas K and 4, and is closed under MP, Nec
and Löb's rule LR, which makes it possible to derive A
from □A → A. Löb's axiom schema L
is □(□A → A) → □A.
It is equivalent to LR over K4. The official definition of GL, provability logic, is K4 plus L.
The formula □⊥ → ⊥ is an example of a formula not in ArTaut.
It also shows that the the logic T is not a sublogic of GL. It is not a sublogic of K4 either. These are in fact
our first unprovability results.
- Oct 17th, 2024
- Soundness and completeness of the calculus GK. The cut-elimination theorem for it. Sequent calculus for the
logic K and a verification that it simulates the Hilbert-style calculus for K.
Homework. Extend the calculus GK for the case where the equivalence connective ≡ is also considered
a basic symbol. The rules should be sound with respect to the truth-value semantics, they should satisfy
the subformula property and the proof of the completeness and cut-elimination theorem should go through.
Hint. One left and one right rule are needed, and both are supposed to be binary.
- Oct 10th, 2024
- Sequent calculus GK for classical propositional logic. The corresponding terminology: sequent, antecedent,
succedent, principal, active and side formulas, initial sequents, context sensitive and context insensitive
variants of binary rules.
Homework. Find a proof of the
sequent 〈 A → B ⇒ ¬A ∨ B 〉.
- Oct 3rd, 2024
- The traditional modal logics K, T, K4, S4 and S5. Their Hilbert-style calculi. Every modal formula
is T‑equivalent to ⊤, or to ⊥, or to a formula not containing the symbols ⊤ and ⊥.
The formulas □□A and □A, and also the formulas
◇◇A and ◇A,
are S4‑equivalent. Thus in S4 every modality followed by the same modality can be equivalently dropped.
The formulas □◇□A → □□A,
□A → ◇□A
and ◇□A → □◇□A are provable
in S5. Indeed, the first can be obtained from the symmetric form of axiom 5 using Thm K(a),
the second is an instance of the symmetric form of axiom T, and the third is an instance of
schema 5. A tautological consequence of the three formulas
is □A → □□A. Thus S5, defined
as T plus 5, is in fact an extension of S4.
Homework. (a) Fill the missing part in the proof that □ commutes with conjunction in K.
(b) The schema A → □◇A
is known as schema B. Prove that B and 5 are equivalent over S4.
Hint. Substitute ◇A for A in schema B.
Then prove □◇◇A → □◇A
using the symmetric form of 4 (which is already known to be provable in S5).
Properties of axiomatic theories
Exams
Připravte si prosím řešení 21 cvičení z nedávno
aktualizovaného seznamu a ke zkoušce přineste jejich seznam (jen čísla). Pokud si přinesete i samotná řešení,
můžete do nich na začátku krátce nahlédnout.
Course contents in Fall 2024/25
- 9. ledna 2025
- Pro každé m>0 existují množiny
v Σm – Πm.
Jejich komplementy jsou v Πm – Σm.
Aritmetická hierarchie tedy nekolabuje. Pro každé m>0 také existují Σm‑kompletní a
Πm‑kompletní množiny. Množina Th(ℕ) všech sentencí platných v ℕ
není v žádné Σm. Je to tedy nearitmetická množina. Z toho plyne jednoduchá
verze První Gödelovy věty: je-li T rekurzívně axiomatizovatelná teorie v aritmetickém jazyce taková,
že ℕ ⊧ T, pak T je neúplná.
Rekurzívně neoddělitelné dvojice RE množin.
- 7. ledna 2025
- Přehled rekurzívně-teoretických pojmů a vztahů mezi nimi.
- 19. prosince 2024
- M-převeditelnost. Univerzální relace pro nějakou třídu množin. Existuje univerzální relace pro třídu
všech Δ0 podmnožin množiny N, která je Δ1.
Z toho plyne, že pro každé nenulové m existuje univerzální relace pro třídu
všech Σm podmnožin množiny N, která sama je Σm.
- 17. prosince 2024
- Párovací funkce (tj.
funkce [n,k] ↦ 〈n,k〉),
k ní inverzní funkce l a r a také různé syntaktické operace jako substituce za volnou proměnnou nebo
připsání negace na začátek (textového řetězce) jsou příklady rekurzívních funkcí. Množina q‑tic
je RE, právě když je definičním oborem nějaké částečně rekurzívní funkce. Množina přirozených čísel
je RE, právě když je prázdná nebo je oborem hodnot nějaké rekurzívní funkce.
- 12. prosince 2024
- Částečně rekurzívní a rekurzívní funkce. Skládáním (substitucí) částečně rekurzívních funkcí vznikne opět
částečně rekurzívní funkce. Definiční obor i obor hodnot částečně rekurzívní funkce jsou RE množiny.
Rekurzívní funkce má rekurzívní (tj. Δ1) graf. Základní metodou pro důkaz, že
funkce f je (částečně) rekurzívní, zůstává ověření, že její graf je Δ0.
- 10. prosince 2024
- Craigův trik. Rekurzívně axiomatizovatelné teorie. Rekurzívní (tj. Δ1) množiny.
Rozhodnutelné teorie. Když T je rekurzívně axiomatizovatelná a úplná, pak je rozhodnutelná. Teorie
DO, DNO a SUCC jsou rozhodnutelné, a všechny jejich modely jsou rozhodnutelné struktury. Jedno z cvičení
(29 při dosavadním číslování) ukazuje příklad teorie, která je rozhodnutelná ale neúplná.
- 5. prosince 2024
- Pokud τ je Σ‑formule, pak Proofτ(x,w)
i Prτ(x) jsou Σ‑formule. Pokud m≠0, pak
jak třída všech Σm podmínek, tak třída všech Πm podmínek
je uzavřena na konjunkci, disjunkci a omezenou kvantifikaci. Navíc Σm je uzavřena
na existenční kvantifikaci a Πm je uzavřena na univerzální kvantifikaci.
Z toho plyne, že každá množina, kterou definuje Σ‑formule, je RE. Takže když existuje
Σ‑formule, která definuje množinu axiomů teorie T, pak Thm(T) je RE.
Pro teorie DO, SUCC, LO, DNO a také pro každou teorii, která je axiomatizovaná pomocí konečně mnoha
axiomů plus případně konečně mnoha schémat, existuje dokonce Δ0‑formule, která definuje
množinu jejích axiomů.
- 3. prosince 2024
- Formule Proofτ(x,w), Prτ(x)
a Con(τ). Pokud τ definuje T, pak
Proofτ(x,w) definuje množinu všech dvojic [φ,m]
takových, že m je důkaz formule φ v T, a Prτ(x)
definuje množinu všech formulí dokazatelných v T. Pokud τ je Δ0, pak
Proofτ(x,w) je Δ0,
Prτ(x) je Σ1 a Con(τ) je Π1.
Aritmetická hierarchie.
- 28. listopadu 2024
- Pro všechny syntaktické pojmy od termů a formulí k logickým axiomům (a případně k numerálům
a k uzávěru formule) existují Δ0‑formule (Term(t), Fla(z) atd.), které je
definují v ℕ.
- 26. listopadu 2024
- Kódování textových řetězců pomocí přirozených čísel. Operace s řetězci: určení délky,
určení x-tého symbolu, spojení (konkatenace) řetězců, počet výskytů určitého symbolu.
Všechny tyto operace (podmínky) jsou Δ0, což lze dokázat použitím
zatím nedokázaných faktů: graf
funkce [x,z] ↦ zx
je Δ0 a graf funkce x ↦ NPB(x)
(která určí počet pozitivních bitů v zápisu čísla x) je Δ0 také.
Vyvážené (balanced) řetězce.
- 21. listopadu 2024
- Předběžná úvaha o budoucí definici algoritmu: algoritmicky rozhodnutelné množiny musí zahrnout
všechny Δ0 množiny, a algoritmicky počitatelné funkce musí zahrnout
všechny funkce, jejichž graf je Δ0. Počítačově přesný zápis termů
a formulí, neboli syntaktické objekty chápané jako textové řetězce (čili možné vstupy algoritmů).
- 19. listopadu 2024
- Eliminace kvantifikátorů je užitečná nejen jako metoda pro prokazování úplnosti teorií, ale
poskytuje také informaci o množinách definovatelných ve strukturách. Δ0 množiny
(relace) jako množiny definovatelné Δ0‑formulemi.
- 14. listopadu 2024
- Ještě dva příklady neaxiomatizovatelných tříd: všechny silně souvislé orientované grafy a všechny
dobře uspořádané množiny. Definovatelné množiny ve strukturách.
- 12. listopadu 2024
- Struktura nestandardního modelu teorie Th(ℕ). Má-li teorie T neomezeně
velké konečné modely, pak má i nekonečné modely. Z toho plyne, že je-li L libovolný jazyk,
pak třída všech konečných struktur pro L není axiomatizovatelná. Z toho je dále jasné,
že její komplement čili třída všech nekonečných struktur, o kterém víme, že axiomatizovatelný je,
není konečně axiomatizovatelný. Löwenheimova-Skolemova věta "směrem nahoru", plná verze:
má-li T v L modely, pak má i modely mohutnosti
nejvýše |L| + ℵ0; má-li navíc nekonečné modely,
pak má i modely každé mohutnosti od |L| + ℵ0
výše.
D. úkol. Cvičení 15 v seznamu nahoře.
- 7. listopadu 2024
- Presburgerova aritmetika je teorie struktury 〈N,+,0,s〉 a z literatury je
o ní známo, že umožňuje eliminaci kvantifikátorů. Axiomatizovatelné (elementární) a konečně axiomatizovatelné
třídy struktur. Komplement konečně axiomatizovatelné třídy je opět konečně axiomatizovatelná třída.
Teorie Th(ℕ) má i nestandardní modely.
- 5. listopadu 2024
- Teorie DOS připouští eliminaci kvantifikátorů a je tedy úplná. Z toho plyne, že i
teorie DO je úplná. Zvláštním případem konzervativního rozšíření teorie je definiční rozšíření (rozšíření
o definice). Rozdíl mezi konzervativním rozšířením a rozšířením o definice ale nehraje roli
v důkazech úplnosti.
- 31. října 2024
- Rozšíření teorie a podteorie. Expanze struktury. Postačující podmínka pro to, aby rozšíření S
teorie T bylo konzervativní: každý model T má expanzi, která je modelem S.
Teorie DOS je konzervativním rozšířením jak teorie SUCC, tak teorie DO.
- 29. října 2024
- Teorie SUCC umožňuje eliminaci kvantifikátorů, a je tedy úplná. Teorie DO diskétního lineárního
uspořádání (discrete order). Jejím preferovaným modelem je struktura 〈N,<〉, kterou
značíme ω. Operace s lineárně uspořádanými množinami: λ* je struktura získaná
z λ obrácením všech šipek, λ + θ sestává
z disjunktních kopií struktur λ a θ, uvnitř nichž je uspořádání
zachováno beze změny, avšak navíc jsou všechny prvky v λ menší než všechny prvky
v θ, a konečně λ · θ
vznikne tak, že v θ nahradíme každý prvek disjunktní kopií struktury λ.
Je-li λ libovolné lineární uspořádání, pak
ω + (ω* + ω) · λ je
model teorie DO.
- 24. října 2024
- Podstatné kroky v důkazu, že teorie SUCC umožňuje eliminaci kvantifikátorů. Z lemmatu 2
(je-li φ konjunkce literálů, pak ∃xφ je ekvivalentní s otevřenou formulí)
zbývá dořešit poslední případ, kdy každý literál ve φ obsahující x je
negativní, vpravo od nerovnítka se v něm nevyskytuje x a vlevo od nerovnítka je v něm
term S(m)(x) vždy se stejným m.
- 22. října 2024
- Teorie SUCC a DNO. Vaughtův test, jeho nikoliv nejsilnější varianta: má-li T nejvýše spočetný jazyk
a je bezesporná, pak je-li navíc ℵ0‑kategorická a nemá konečné modely (dokonce stačí, že
každé dva její nejvýše spočetné modely jsou spolu izomorfní), pak je úplná. Takže například DNO je úplná.
Nechť γn pro n>0 je
sentence ∀x1 . . ∀xn∃y(y≠x1 & . . & y≠xn). Pak
{γn ; n>0 } je úplná teorie
(s prázdným jazykem), což je řešení cvičení 10 a 13. Také cvičení 12 bylo na přednášce vyřešeno.
Teorie {γ2,¬γ3} je úplná, ovšem nesplňuje podmínku, že
nemá konečné modely. O teorii SUCC umíme dokázat, že není ekvivalentní s žádnou svou konečnou podteorií.
Plánem do budoucna ale je dokázat, že není ekvivalentní s vůbec žádnou konečnou teorií.
Přesně totéž lze říci o teorii z cvičení 10.
- 17. října 2024
- Věta o úplnosti. Slabá verze Löwenheimovy-Skolemovy věty. Tzv. Skolemův paradox: má-li teorie množin
modely, pak má i nejvýše spočetné modely (je ale jasné, že konečné modely nemá). Úplné teorie.
Množiny Thm(T) a Ref(T) sentencí dokazatelných a vyvratitelných v T.
Pokus o přehlednou axiomatizaci struktury 〈N,0,s〉, čili o nahrazení množiny Th(ℕ)
jednodušší množinou axiomů.
- 15. října 2024
- Korektnost pravidel kalkulu HK vůči sémantice klasické predikátové logiky. Relace důsledku.
Větu o korektnosti lze pro teorie formulovat také takto:
když T ⊢ φ,
pak T ⊧ φ.
- 10. října 2024
- Izomorfní a neizomorfní struktury. Ohodnocení proměnných, Tarského definice, platnost formule
ve struktuře. Výroková část kalkulu HK je korektní vůči sémantice predikátové logiky s rovností
v tom smyslu, že v každé struktuře každé ohodnocení splňuje každou tautologii a když ohodnocení
splňuje implikaci i její premisu, splňuje i její závěr.
D. úkol. Vyřešte sémantickou část cvičení 1 (pdf soubor na webu kursu): pro formuli vzniklou obrácením
nejvnějšnější implikace existuje ve všech pěti případech existuje struktura, ve které ta formule neplatí.
Nebo vyřešte cvičení 9, tam možná jsou zajímavější konstrukce struktur.
- 8. října 2024
- Věta o dedukci v predikátové logice. Sporné a bezesporné teorie. Věta o korektnosti jako základní
a možná jediný nástroj pro prokazování nedokazatelnosti. Struktury. Příklady, prominentní číselné struktury.
- 3. října 2024
- Doprohlédnutí hilbertovského kalkulu HK (či HKe) pro klasickou predikátovou logiku
s rovností: axiomy rovnosti, pravidla generalizace.
D. úkol. S využitím tautologických důsledků a případně neformálních důkazů zdůvodněte dokazatelnost sentencí
∀x(P(x) → Q(x)) → (∃xP(x) → ∃xQ(x),
∃x∀yR(x,y) → ∀y∃xR(x,y)
a ∃x(P(x) → ∀yP(y)).
Návod. Začněte s tautologií ¬P(z) → (P(z) → ∀yP(y)) a s instancí axiomu specifikace, která má v premise závěr této implikace.
Méně názorný ale o dost kratší důkaz lze také založit na tom, že pravidlo generalizace aplikujete na
formuli ¬∃x(P(x) → ∀yP(y)) → P(y).
- 1. října 2024
- Přehled logické syntaxe: od termů k axiomatickým teoriím. Jednoduchá teorie s axiomy
Q1 a Q2. Logické axiomy. Použití tautologií a tautologických důsledků v predikátové logice,
neformální důkazy.
Arithmetics and algorithms
Exams (Czech)
Ke zkoušce si prosím připravte (přineste) řešení osmnácti libovolně zvolených
cvičení (i s vysvětlením matematického či algoritmického pozadí). Zkouška pak pokračuje prodiskutováním
některého důkazu. Kromě termínů vypsaných v SISu se lze domluvit i na jinou dobu, ale ve středu obvykle mohu
až tak od 17h, a v pátek pouze ráno a pouze možná. Všechny termíny lze využívat i jako konzultace.
Course contents in Spring 2024/25 (Czech)
- 25. dubna 2025
- Mersennova prvočísla a výsledek F. Colea z roku 1904. Úlohy ve třídě NP. Řády prvků v grupách.
Když m je prvočíslo, pak v grupě Φ(m) existují prvky, jejichž řád je φ(m).
Na této (v přednášce nedokázané) větě lze založit metodu pro prokazování, že dané (velké) číslo je prvočíslo.
Jinak řečeno, lze na ní založit důkaz, že úloha Primes je v NP. Z doslechu
víme, že je dokonce v P, to ale má velmi obtížný důkaz.
- 24. dubna 2025
- Počítání s modulárními reprezentacemi, čínská zbytková věta. Kryptografická metoda RSA.
- 10. dubna 2025
- Zobecněná Eulerova věta: umocníme-li v komutativní grupě s n prvky libovolný prvek a
na n‑tou (tj. vynásobíme-li a se sebou n−1‑krát) dostaneme
neutrální prvek oné grupy. Takže v každé grupě Φ(m)
platí aφ(m) = 1. Z toho speciálně
plyne Malá věta Fermatova: je-li m prvočíslo a je-li a nenulový prvek
struktury ℤm, pak v ℤm (neboli ve Φ(m))
platí am−1 = 1.
- 3. dubna 2025
- Ekvivalentní podmínka pro nesoudělnost: čísla (prvky libovolného oboru integrity) x a y
jsou nesoudělná, právě
když ∀z(x | yz → x | z).
Umocňování modulo m je polynomiálně počitatelná operace.
D. úkol. Na základě znalosti důkazu týkajícího se nesoudělnosti (a s opětovným využitím Bézoutovy věty)
dokažte, že x je ireducibilní, právě když je prvočíslem.
- 27. března 2025
- Rozšířený (čtyřsloupcový) Eukleidův algoritmus. Jeho matematický důsledek: Bezoutova rovnice, tj.
rovnice tvaru ax + by = c, má v ℤ
řešení právě tehdy, když c je dělitelné (každým, čili některým největším, čili každým největším)
společným dělitelem čísel a a b. Eukleidův algoritmus nalezne některé řešení,
pokud existuje. Algoritmický důsledek: o invertibilitě prvku x v ℤm
lze rozhodnout v polynomiálním čase. Navíc, pokud prvek x invertibilní je, prvek k němu
inverzní lze také nalézt v polynomiálním čase. V ℤ
platí sentence ∀a∀b∃x∃y(ax + by | a & ax + by | b), takže ji lze považovat
za dodatečný axiom, který lze přidat k axiomům oboru integrity.
D. úkol. S využitím Eukleidova algoritmu vyřešte cvičení 6 nebo 7 v seznamu nahoře.
- 20. března 2025
- Vlastnosti relace dělitelnosti v oborech integrity. Ireducibilní čísla, nesoudělnost, prvočísla.
Číslo (prvek oboru integrity) 1 a každý jeho dělitel jsou nesoudělní s každým číslem. Číslo 0 je soudělné
s každým číslem, které není invertibilní. Ireducibilní číslo je nesoudělné s každým číslem kromě svých
násobků. Eukleidův algoritmus a z něj odvozená definice největšího společného dělitele. Tento algoritmus
pracuje v polynomiálním čase.
D. úkol (1) Dokažte, že polynom x2 + 1
je v ℚ[x] ireducibilní.
D. úkol (2) Dokažte, že každé prvočíslo je ireducibilní.
- 13. března 2025
- Obory integrity a tělesa. Nenulovými prvky v tělese lze krátit. V oboru integrity také,
ale má to úplně jiný důkaz. Eulerova grupa přirozeného čísla m>1, Eulerova funkce.
Dělitelnost v oborech integrity. Relace dělitelnosti je tranzitivní
a reflexivní, ale mohou existovat různé prvky, z nichž každý dělí ten druhý. Takovým prvkům říkáme
asociované. Nula je jediným prvkem, který je dělitelný nulou, dělitelé jedničky jsou právě
ty prvky, které jsou invertibilní. Když x a y jsou asociované, pak některý z nich
(tím pádem ovšem každý z nich) lze z druhého získat vynásobením nějakým invertibilním v.
- 6. března 2025
- Grupy (Abelovy) a (komutativní) okruhy. Invertibilní prvky v monoidech a okruzích.
Modulární aritmetika.
- 27. února 2025
- Úloha GCD, neboli úloha nalézt největšího společného dělitele dvou daných přirozených čísel.
Komutativní monoidy jako jedna ze základních algebraických struktur.
- 20. února 2025
- Úloha a algoritmus jako základní pojmy teoretické informatiky. Časové nároky
algoritmů. Školní algoritmus pro úlohu Mult neboli pro násobení pracuje
v kvadratickém čase, školní algoritmus pro sčítání dokonce v lineárním čase. Pro algoritmy,
které pracují v čase linárním, kvadratickém, kubickém atd. máme souhrnný název
polynomiální algoritmy. Úlohou, pro kterou polynomiální algoritmus neexistuje, je
pravděpodobně Factoring, čili úloha nalézt prvočíselný rozklad daného čísla.
Ale dokázané to není. Nalezení důkazu, že takový algoritmus opravdu neexistuje, je otevřeným
problémem. Dva algoritmy uvedené v přednášce, z nichž jeden dělí dané a různé od nuly a jedničky
všemi čísly d splňujícími podmínku
2 ≤ d < a a druhý pouze čísly d splňujícími podmínku
4 ≤ d2 ≤ a, pracují v exponenciálním čase,
takže polynomiální rozhodně nejsou.
Huge number calculator
The calculator BNCalc.pdf is implemented
as a (set of scripts behind a) pdf document and can be used for operating with
really huge integers. Note that there are some undocumented key combinations
that make it easier to repeat the given operation.
The "result" text field in the "Factoring" page, marked by an arrow in this
image, accepts Shift‑M (or Shift‑B with the same
meaning).
Also, the result text field on the preceding page accepts Shift‑M and Shift‑B.
Incompleteness and Gödel Theorems
Here is an (updated May 17th, 2025) list
of exercises.
Exams (Czech)
Ke zkoušce si prosím připravte řešení dvanácti (z celkového počtu čtrnáct) cvičení.
Důkaz Solovayovy věty o úplnosti logiky GL je ke zkoušce nepovinný, ale lze jím případně nahradit
něco z ostatních požadavků.
Course contents in Spring 2024/25
- 6. dubna 2025
- Dokončení Solovayova důkazu věty o aritmetické úplnosti logiky GL. Nepodařil se úmysl buď se samostatně zabývat
Rosserovou sentencí, nebo ji vyložit jako speciální případ Solovayova důkazu (který začíná z kripkovského
modelu, jehož rámec sestává ze dvou nesrovnatelných prvků). Tomuto budou možná věnována nějaká cvičení,
ale jejich seznam bude aktualizován a požadavek ke zkoušce upřesněn až později.
- 5. května 2025
- Kromě PA‑tautologií má smysl uvažovat i (větší množinu) všech ℕ‑tautologií.
ℕ‑tautologie nejsou uzavřeny na pravidlo Nec, ale obsahují všechny modální formule
tvaru □A → A, tj. všechny instance
schématu reflexe.
- 29. dubna 2025
- Löbova věta má i o něco přímočařejší důkaz, než je původní Löbův: lze ji odvodit z Druhé
Gödelov věty. Z Löbovy věty plyne aritmetická korektnost modálního Löbova pravidla. Protože rozšíření
logiky K4 o Löbovo pravidlo je jednou z ekvivalentních axiomatizací logiky dokazatelnosti (tj. logiky GL),
logika GL je korektní vůči aritmetické sémantice. Jedna z aplikací tohoto faktu: některé autorererenční
rovnice (v tom Gödelova, Henkinova i Löbova) mají jednoznačně určené řešení v tom smyslu,
že každá dvě řešení jsou PA–ekvivalentní.
- 24. dubna 2025
- V PA jsou možné i další důkazy bezespornosti, například Robinsonovy aritmetiky. Bylo by k tomu
ale potřeba zabývat se tzv. částečnými definicemi pravdy, a pak větou o eliminovatelnosti řezů pro klasickou
predikátovou logiku. Důkaz Löbovy věty podle Löbova článku z roku 1955.
- 22. dubna 2025
- Normální (tzv. Tarského) sémantika je formalizovatelní v ZF, a v ZF je dokazatelná i věta o korektnosti:
teorie, která má model, je bezesporná. V ZF je dokazatelné i to, že
{ z ; π(z) } má model.
Takže ZF ⊢ Con(π). Z Druhé Gödelovy věty plyne, že
existence modelu teorie množin v ZF dokazatelná není. I v PA lze (pomocí ad hoc sémantiky) dokázat
bezespornost určitých (slabých) teorií.
- 17. dubna 2025
- Druhá Gödelova věta: pokud T je bezesporné rozšíření PA a τ(z)∈Σ
definuje T, pak T⊬Con(τ). Některé souvislosti: Hilbertův
program, modální logika.
- 15. dubna 2025
- Několik bezprostředních důsledků Löbových podmínek. Slabá reprezentovatelnost funkcí
(s Δ0‑definovatelným grafem) v Q. Věta o autoreferenci.
- 14. dubna 2025 (nahrazení přednášky z 13. května)
- Formalizace dokazatelnosti a bezespornosti v PA. Tvrzení, která mají syntaktický důkaz, například
větu o dedukci nebo to, že ve sporné teorii lze dokázat cokoliv, lze dokázat v PA. Löbovy podmínky
(Löb's derivability conditions).
- 10. dubna 2025
- Nejen mocniny dvojky, ale i umocňování jako funkci dvou proměnných, a také funkci NPB (number of
positive bits) lze formalizovat v PA. Takže lze formalizovat i syntaktické pojmy.
- 8. dubna 2025
- Eukleidův důkaz, že ireducibilních čísel je nekonečně mnoho, lze (s jistou opatrností a
s přeformulováním některých argumentů) formalizovat v PA. Také Bézoutovu větu lze v PA formalizovat,
z čehož je (v PA) jasné, že ireducibilní čísla jsou přesně ta, která jsou prvočísly.
- 3. dubna 2025
- Schéma LNP (princip nejmenšího prvku) je se schématem indukce ekvivalentní nad Robinsonovou
aritmetikou obohacenou o jeden dodatečný axiom. Ale lze ukázat (konstrukcí jednoduchého modelu), že
ten dodatečný axiom je nutný. V Peanově aritmetice lze dokázat větu o dělení se zbytkem.
První kroky směřující k tomu, že v PA lze formalizovat Eukleidův důkaz, že ireducibilních čísel
je nekonečně mnoho.
- 1. dubna 2025
- Peanova aritmetika PA. Parametrická a neparametrická indukce. V PA lze dokázat, že obě operace
a uspořádání mají očekávané vlastnosti.
- 27. března 2025
- Teorie je podstatně neúplná, právě když je podstatně nerozhodnutelná. Odstraněním kteréhokoliv
z prvních sedmi axiomů Robinsonovy aritmetiky vznikne teorie, která není podstatně nerozhodnutelná.
Konečné rozšíření rozhodnutelné teorie je rozhodnutelné. Z toho plyne, že odebráním axiomů
z Robinsonovy aritmetiky vždy vznikne teorie, která je nerozhodnutelná. Množina všech logicky platných formulí
v aritmetickém jazyce je algoritmicky nerozhodnutelná.
- 25. března 2025
- Rosserovo zobecnění První Gödelovy věty: každé rekurzívně axiomatizovatelné rozšíření T
Robinsonovy aritmetiky je neúplné a nerozhodnutelné. Existují Σ1‑
a Π1‑sentence, které jsou nezávislé na T. Že Thm(T) je
Σ1‑kompletní, je pravda také, ale z daného důkazu to nevyšlo.
- 20. března 2025
- Strukturální důkaz První Gödelovy věty. Každé rekurzívně axiomatizovatelné
Σ1‑korektní rozšíření T Robinsonovy aritmetiky je neúplné a nerozhodnutelné.
Thm(T) je Σ1‑kompletní. Existují nezávislé Σ1‑
a Π1‑sentence.
- 18. března 2025
- Dosazením numerálů do Δ0‑formule vždy vznikne sentence, která je v Q
dokazatelná nebo vyvratitelná (podle toho, zda platí nebo neplatí v ℕ). Dosazením numerálů
do Σ‑formule vždy vznikne sentence, která pokud platí v ℕ, je v Q
dokazatelná. Z toho plyne (i), že Δ0‑sentence nemůže být na Q nezávislá
a (ii) že Σ‑sentence platná v ℕ je vždy v Q dokazatelná. Přitom (ii)
bylo dokázáno jako důsledek (i), ale stojí za zmínku, že (i) plyne z (ii): jak
Δ0‑sentence, tak její negace jsou Σ. Všem těmto tvrzením se říká věta
o Σ‑úplnosti Robinsonovy aritmetiky.
- 13. března 2025
- Dokazatelnost v Q. Schémata týkající se numerálů, která lze interpretovat tak, že z hlediska
uspořádání nemohou nestandardní prvky modelu Robinsonovy aritmetiky být mezi standardními, ani nemohou
se standardními být nesrovnatelné, ale musí být za nimi. Atomická sentence je vždy v Q dokazatelná
nebo vyvratitelná.
- 11. března 2025
- Robinsonova aritmetika Q. Její jednoduchý model se dvěma nestandardními prvky, z něhož je jasné,
že například asociativita a komutativita operací nebo tranzitivita uspořádání nejsou v Q dokazatelné.
Q1–Q5 je konzervativní nad Q1–Q3, ale Q1–Q7 není konzervativní nad Q1–Q5.
- 6. března 2025
-
Pokračování úvah o množinách K a K0: ani K0 není rekurzívní, protože
K je na ni m‑převeditelná; dokonce platí, že každá RE množina je m‑převeditelná na K0,
což jinými slovy znamená, že K0 je Σ1‑kompletní. Existence
rekurzívně neoddělitelných dvojic disjunktních RE množin.
- 4. března 2025
- Ackermannova funkce. M‑převeditelnost. Vlastnosti množin K a K0: zatím je jasné, že
obě jsou RE a K není rekurzívní.
- 27. února 2025
- Operace primitivní rekurze. Zobecněná primitivní rekurze. Dodatek k větě shrnující souvislosti
mezi RE a Δ1 množinami a (částečně) rekurzívními funkcemi:
nekonečná množina A ⊆ N je Δ1,
právě když je oborem hodnot nějaké rostoucí rekurzívní funkce, a je RE, právě když je
oborem hodnot nějaké prosté rekurzívní funkce.
- 25. února 2025
- Souvislosti mezi RE a Δ1 množinami a (částečně) rekurzívními
funkcemi. Operací substituce a minimalizace vznikne z částečně rekurzívních funkcí opět částečně rekurzívní funkce.
- 20. února 2025
- Rekurzívní množiny. Craigův trik, rekurzívně axiomatizovatelné teorie. Každá rekurzívně axiomatizovatelná
úplná teorie je rozhodnutelná. Postova věta, věta o projekci.
- 18. února 2025
- Přehled základních pojmů z vyčíslitelnosti a jejich souvislostí s logikou. Δ0-formule,
důležité Δ0 podmínky týkající se čísel nebo syntaktických objektů,
formule Proofτ(x,y). RE podmínky,
uzavřenost na operace, univerzální RE relace, formule Prτ(x).
Chapters in Classical Logic
About
A seminar partly based on students' presentations, devoted to various
topics in metamathematics, non-classical logics, and proof theory.
The topics usually include: Provability Logic,
independence of the Paris-Harrington combinatorial
principle over Peano arithmetic,
relations between ZF, GB and the Kelly-Morse set theories,
upper and lower bounds for cut-elimination in
classical predicate logic, decision procedures
for intuitionistic propositional logic.
List of topics (in Czech).
SIS: ALG500003.
Exams (Czech)
Ke zkoušce je třeba zvládnout témata dle vlastního výběru, která pokrývají
15 dvouhodinovek. Vlastní přednáška se do počtu 15 počítá trojnásobně.
Course contents in 2024/25 (Czech)
- Intuicionistická predikátová logika, různá její rozšíření (Marie Fojtíková, 6.5. a 13.5.)
- Sémantika intuicionistické predikátové logiky. Silnější varianta relace ≠, neboli relace anglicky
zvaná apartness. Dodatečná schémata, jejichž přijetím (přidáním) vzniknou tzv. intermediate logics (česky
snad mezilogiky?). Např. schéma DNS demonstruje, že pro intuicionistickou predikátovou logiku neplatí
vlastnost konečných modelů (finite model property). Schéma CD (constant domains) platí ve všech kripkovských
modelech, v nichž všechny vrcholy mají tutéž nosnou množinu. Schéma ED se objevilo v souvislosti s úvahami,
zda (a pokud ne, tak v jakém rozšíření intuicionistické logiky) lze existenční kvantifikátor vyjádřit
pomocí ostatních symbolů. Zkoumání některých těchto dodatečných principů je také motivováno otázkou, které
z prenexních operací jsou intuicionisticky korektní.
K tomu četba.
- Riegerův-Nishimurův svaz (Timea Cochová, 29.4. a 6.5., dvě přednášky)
- Formule En a Dn jsou definovány rekurzí, jsou sestaveny
pomocí disjunkce a implikace ze symbolu ⊥ a atomu p a mají vlastnost, že formule sestavená
z některých dvou z nich pomocí disjunkce, implikace nebo konjunkce je ekvivalentní opět s některou
z nich. Vztahy mezi nimi udává svaz (Heytingova algebra) zvaný R.-N. svaz. Dále R.-N.–žebřík
je kripkovský model, který demonstruje, že žádné jiné vztahy mezi formulemi
En a Dn neplatí. Speciálně, žádné dvě nejsou ekvivalentní.
K tomu četba.
- Turingovská převeditelnost a Friedbergova-Muchnikova věta (Martin Q. Putzer, 22.4. a 28.4.)
- Rekurzívní funkce, rekurzívní a rekurzívně spočetné množiny, 7 equivalentních definicí. Důkazy o poslední
podmínce: 7 implikuje 3, 5 implikuje 7. Addendum: odstraníme-li z podmínky 7 passus o
neklesavosti v druhé proměnné, získáme ekvivalentní definici
třídy Σ1∪Π1, nahradíme-li neklesavost nerostoucností,
získáme definici třídy Π1. Kleeneova věta o normální formě. Neformální diskuse orákul
a orákulových strojů, formalizace Turingovými funkcionály pro rekurzívně spočetná orákula, neformální vysvětlení
obecného případu. Rozdíl mezi Turingovskou převeditelností a m‑převeditelností. Tvrzení Friedbergovy‑Muchnikovy
věty. Podstata prioritní methody. Četba:
Prolegomena,
kniha André Nies,
Ladislav Strojil, Kučerovy přednášky z vyčíslitelnosti,
kniha Robert I. Soare obsahuje delší ale hezké vysvětlení.
A dodatečně zaslané skriptum.
- Matematická neúplnost v Peanově aritmetice (David Roubínek, od 18.3. do 15.4., čtyři přednášky)
- Konečná a nekonečná Ramseyova věta. Parisovo-Harringtonovo zesílení Ramseyovy věty neboli princip PH: pro
každé k, n a c existuje m, že pro každé obarvení n‑tic
přirozených čísel c barvami existuje homogenní množina H (čili taková, že každá
n‑tice jejích prvků má tutéž barvu), která má alespoň max(k,min(H)) prvků.
Kanamoriho-McAloonův princip KM. Šipkovací notace pro tyto principy. PH i KM jsou dokazatelné v ZF.
V Peanově aritmetice PH implikuje KM.
Instance (PH)n a (KM)n principů PH a KM pro standardní čísla
v PA dokazatelné jsou. Definice indikátoru.
Důkaz, že z KM lze v PA získat nerozlišitelné (nerozlišitelná čísla, indiscernibles) pro formule
s maximálně n+1 volnými proměnnými.
V každém nestandardním modelu Peanovy aritmetiky, v němž platí KM, lze k libovolnému
nestandardnímu prvku a sestrojit řez I, který je modelem PA, obsahuje a
a má následující vlastnost. Nejmenší číslo b takové, že interval [a,b] šipkuje
jistou relaci, je mimo I. Z toho plyne, že v I neplatí KM, a tedy ani PH.
Četba: základními zdroji jsou článek Kanamori-McAloon a kniha od Richarda Keye, přičemž ke studiu je doporučený možná spíš
ten článek. Dále článek Ketonen-Solovay a kapitola Paris-Harrington jsou spíš jen pro nahlédnutí či orientaci v historii.
- Gentzenův důkaz bezespornosti Peanovy aritmetiky, pokračování (Jiří Rýdl, 4.3. a 11.3.)
- Zde je Jiřího handout. Ale tento abstrakt ještě možná bude poupraven. A Jiří
možná na začátku setkání v úterý 2. dubna přednese určité shrnutí.
- Metamatematika teorií množin (Šimon Pošta, 18.2. a 25.2.2025)
- Axiomatika teorií ZF a GB (tato teorie je nověji často označována jako NBG, kde N odkazuje
k von Neumannovi). Axiomy GB jsou obvykle formulovány jako sedm nebo osm jednotlivých axiomů, které do
značné míry odpovídají axiomům ZF, plus jedno schéma (comprehension schema), které zaručuje, že každá
normální vlastnost množin určuje třídu (všech množin, které mají onu vlastnost). Ale GB je
konečně axiomatizovatelná, to schéma lze ekvivalentně nahradit sedmi jeho instancemi. Možná témata ke
zkoušce: (1) ta konečná axiomatizovatelnost (asi ji lze vyčíst z knihy od Sochora), (2) princip reflexe
a nemožnost konečné axiomatizovatelnosti teorie ZF (asi lze vyčíst z knihy od Jecha, a bude to tam velmi
stručné, ale odhadl bych, že bude vhodné to trochu revidovat či doplnit z pohledu logika),
(3) konzervativita GB nad ZF vůči množinovým sentencím (to lze vyčíst
z článku Vopěnka-Hájek, a je také obsaženo v Šimonově handoutu), (4) nedokazatelnost v GB plné indukce pro
přirozená čísla (to je také v článku Vopěnka-Hájek, a navíc je to převyprávěno
v mém článku v Logica Yearbook).
- Pudlákův spodní odhad pro eliminaci řezů (Eliška Schůtová, od 10.12. tři přednášky)
- Pudlákova exponenciální aritmetika.
- Gentzenův důkaz bezespornosti Peanovy aritmetiky (Jiří Rýdl, zatím 26.11. a 3.12.)
- Pro Peanovu aritmetiku lze navrhnout pravidlo gentzenovského kalkulu, které simuluje schéma indukce
a přitom nepracuje se zbytečně složitými formulemi. Prosté důkazy, linie (threads), hranice (boundary)
a hraniční sekventy, finální úsek důkazu.
- Eliminovatelnost řezů v klasické predikátové logice (Martin Georgiu, 12. a 19.11.)
- Regulární formule a sekventy, regulární důkazy. Lemma o redukci: důkaz, jehož posledním krokem
je řez na formuli θ a v němž všechny ostatní řezové formule mají hloubku menší
než θ, lze přepracovat na důkaz téhož sekventu, který má nižší rank než původní důkaz.
- Neefektivnost rezoluce (Timotej Šujan, 22.10. až 5.11., tři přednášky)
- Rezoluční kalkulus. Efektivní a neefektivní výrokové kalkuly.
- Dobrá uspořádání v teoretické informatice (Laura Clowez, 15. a 22.10.)
- Na množině všech konečných multimnožin sestavených z prvků fundovaně uspořádané množiny
lze přirozeným způsobem definovat uspořádání a dokázat o něm, že je také fundované.
To pak lze v některých případech použít k důkazu, že určitý algoritmus se dopočítá na každém vstupu.
McCarthyho 91-funkce.
- Úvod (V. Švejdar, 8.10.)
- Upřesnění programu pro zimní semestr. Timotej, Martin Georgiu a Jiří připravují nebo již mají
připraveny přednášky. Plány nad to existují ale moc určité zatím nejsou. Krátký výklad o univerzálních
relacích pro určitou třídu množin jako pokus o úvod (začátek úvodu) do zamýšlených přednášek
Timoteje nebo Martina Putzera o rekurzívních funkcích.
Interpretation of Gödel incompleteness theorems
About
A seminar based on students' presentations, devoted to reading papers
mainly by Smorynski and Detlefsen.
Here is a course announcement.
SIS: ALGV19006.
Course contents in 2023/24
- Smorynského článek Hilbert's Programme (Adam Fürstenzeller, od 14.12., 2 přednášky)
- Abstrakt (poskytnutý přednášejícím): Smoryńského článek popisuje situaci, ve které se matematika jako
vědecká disciplína ocitla na začátku dvacátého století. Mezi matematiky se vedly diskuse týkající se
formulování samotných základů této vědní disciplíny. Jednou z teorií byl intuicionismus, za jehož
zakladatele se považuje L. E. J. Brouwer, který ve své disertaci (1907) zformuloval základní myšlenky
tohoto směru. Intuicionisté odmítali aktuální nekonečno a využívání aristotelské logiky, zejména zákonu
vyloučení třetího, pro nekonečné objekty. Dalším rozšířeným směrem byl formalismus v čele s Davidem
Hilbertem. Hlavní myšlenkou formalismu je budování bezesporných axiomatických teorií — sad axiomů,
které úplně popisují danou matematickou teorii (věty a axiomy jsou pravdivé, když nejsou ve sporu se svými
důsledky — nemusí se nutně jednat o “evidentní” pravdy).
Názorová rozepře mezi Hilbertem a Brouwerem
je ústředním tématem celého článku. Smoryński důkladně popisuje jak osobní vztah hlavních dvou protagonistů,
tak i ohlasy, které jejich práce vyvolaly. Počátkem dvacátých let získává Brouwer nové stoupence. Jedním
z nich byl také H. Weyl, jehož přednáška z roku 1920 přiměla Hilberta znovu se plně věnovat práci
v oblasti základů matematiky. Společně se svými stoupenci se snaží dokázat bezespornost aritmetiky
(v širším smyslu, zahrnujícím i analýzu a teorii množin) — tzv. Hilbertův program. Ideový spor
mezi Hilbertem a Brouwerem se postupně přesouvá i do osobní roviny. Jeho vrcholem je vyloučení Brouwera
z Matematische Annalen, které inicioval Hilbert.
V průběhu dvacátých let 20. století předkládá
Hilbert rozpracované důkazy Ackermanna a Von Neumanna a zdá se, že důkaz bezespornosti aritmetiky a s ním
i dokončení Hilbertova programu je na dosah ruky. Zvrat však přináší rok 1931 a Gödelovy věty o neúplnosti.
V první z nich Gödel dokázal, že každá bezesporná rekurzivně axiomatizovatelná teorie obsahující aritmetiku
je neúplná (existuje v ní nezávislé tvrzení) a tím prokázal neuskutečnitelnost Hilbertova programu.
- Eckart Menzler-Trott: Logic's Lost Genius — The Life of Gerhard Gentzen (Timea Cochová, od 30.11., 2 přednášky)
- Zaoberali sme sa životným príbehom matematika a logika Dr. habil. Gerharda Gentzena. Od detstva, cez
štúdium a prácu až po jeho tragickú smrť v Prahe. Nahliadli sme k jeho práci a komunikácii
s matematikmi vtedajšej doby, ako boli napríklad Hilbert a Bernays. Z oficiálnych dokumentov,
spovedí blízkych, pracovných a osobných listov sa dozvedáme o jeho charaktere a sledovali sme rozvoj jeho
nápadov a práce. Taktiež sme si priblížili ako vyzerala veda a hlavne matematika a logika v nacistickom
Nemecku a v zvyšku sveta.
Ukážky niektorých listov a dokumentov:
PDF1,
PDF2.
- L. E. J. Brouwer: Life, Art and Mysticism (Šimon Pošta, 23.11., 1 přednáška)
- Brouwerův výchozí bod Smutného světa, role člověka jako individua a jako člena kolektivu, zásadnost
karmického řádu a jeho prohlédnutí skrze přivrácení se k sobě, druhy řečí, pravd a jejich vztah
k vědám, speciálně k logice a matematice. K tomu podrobnější
shrnutí.
- Detlefsenův článek z roku 79 (Timotej Šujan, od 2.11, 1.5 přednášky)
- Abstrakt (poskytnutý přednášejícím): Detlefsen v první části článku kritizuje takovou skeptickou
interpretaci (SI) Gödelovy druhé věty (G2), která by se snažila dojít ke skeptickému závěru, že víru
v konzistenci teorie T nelze odůvodnit důkazem sentence Con(T). Tvrdí, že tento
závěr z G2 žádným zřejmým způsobem neplyne, a tedy je potřeba dokázat určité pomocné předpoklady
SUP1 a SUP2. Následně se snaží ukázat, že platnost SUP1 vyvrací původní SI —
v jeho argumentu jsou ústřední pojmy jako reflexivní teorie
či (jeho vlastní pojem) epistemicky kompaktní teorie. V druhé části článku se snaží upravit SI tak,
aby unikla ze spárů jeho kritiky, avšak následně i takovou upravenou SI odmítá jako nepodloženou.
V třetí části krátce odmítá jako nepodloženou Resnikovu interpretaci G2 v kontextu
“nejsilnějšího/nejsložitějšího systému, který jsme ještě ochotní vážně zkoumat”, a to i kvůli
nejasnému popisu takového systému. V závěrečné části se pak snaží zachránit Hilbertův program tak, že
představuje tzv. omezené ω-pravidlo, které je dle něj v souladu s finitními metodami, které
Hilbertův program vyžaduje, a tvrdí, že např. Con(PA) je dokazatelné z PA+(ω-pravidlo).
- Gödelův článek z roku 1931 (L. Clowez, od 19.10., 2.5 přednášky)
- Kódování logické syntaxe, které je založeno na prvočíselných rozkladech přirozených čísel.
Definice kalkulu poměrně podobná dnešní definici kalkulu hilbertovského. Gödel pracuje s axiomatickou
teorií, která odráží takzvanou teorii typů. Viditelný rozdíl vůči dnešním přístupům je to, že nepracuje
s nějakým předem fixovaným jazykem. Pouze trvá na tom, že k dispozici jsou symboly pro nulu a následnickou
funkci. Článek pracuje s “rekurzívními” funkcemi, ale definici se shoduje s tím, čemu
se dnes říká primitivně rekurzívní funkce (dnes víme, že rekurzívní funkce lze ztotožnit s funkcemi
algoritmicky počitatelnými a je jich víc než primitivně rekurzívních). Jako celkem věrohodná tedy vypadá
historická hypotéza, že kromě vět o neúplnosti je článek důležitý také tím, že v něm byly zavedeny
primitivně rekurzívní funkce.
- Dnešní pohled na Gödelovy věty (V. Švejdar, 2 týdny)
- Trochu životopisných údajů ke Gödelovi. Ingredience důkazu jeho vět o neúplnosti: kódování syntaxe,
numerály, definovatelné množiny, Σ-formule a věta o Σ-úplnosti, predikát dokazatelnosti, věta
o autoreferenci.
Other activities
TeX/LaTeX, pdf, ...
FBUsersSetup
The Firebird SQL server comes with a command line utility
gsec for manipulating database users. Using it, one can add, delete, or modify server's
users, where a modification practically means a password change.
FBUsersSetup.exe is written as an Inno Setup Windows
installer*)Unlike normal installers, it does not
write anything to the registry and does not leave any trace on your computer. So no
deinstallation is provided/needed.
and it basically is a gui wrapper for the gsec utility.
As such, it has little additional functionality in comparison to gsec.
However, it is easy to use, it can modify users on any computer in or outside the local network,
it never gets confused if there are parallel instances of Firebird running on the local computer,
and it can detect the properties of the local Firebird(s).
The utility is rather self-explanatory, the essential dialog pages being
- the selection
of a db server
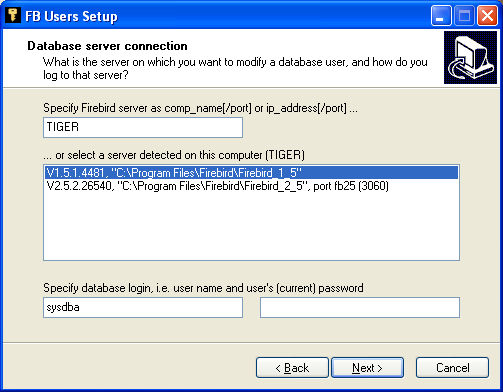
On the local computer, TIGER, there are two parallel instances of Firebird.
One communicates through the standard port 3050, the other through port fb25 that translates
to 3060 in the services file. The user can click on one of them in the listbox,
or say something else. Assume that, since he wants to modify users on the computer JUPITER where
Firebird communicates through port 3060, he deleted the text "TIGER" in the upper text field
and typed "JUPITER/3060" instead. In the two bottom text fields he has to specify the admin login.
In most cases, the admin would be SYSDBA. However, in Firebird 2.0 and later any user can
change his own password.
, and then
- a user action
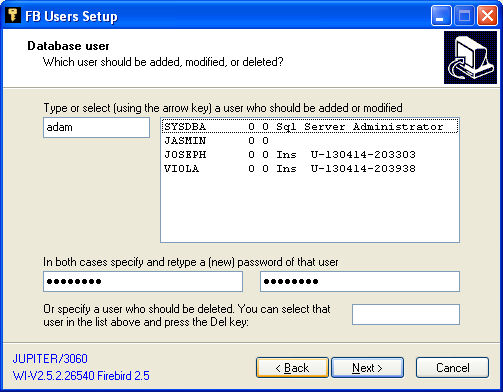
The version of Firebird addressed as JUPITER/3060 is 2.5.2. Besides SYSDBA, there
are three other database users on that server. Since database user's first and last names are hardly ever needed,
FBUsersSetup somewhat misuses these data and codes the current time into them: JOSEPH and VIOLA
were inserted on Apr 14th, 2013. JASMIN was not inserted using FBUsersSetup and so her
first and last names are unknown. A new database user ADAM is now about to be inserted.
on that server.
DBUSubst
The utility DBUSubst.exe
can substitute one Firebird database user for
another. A substitution of user M for existing user D in a database
means that M becomes an owner of all database objects that user D owned,
he inherits all privileges that were granted to D, and he becomes a grantor
of all privileges that D granted. After being substituted out, user D
grants and is granted nothing, and owns no database object. If D was
an owner of a database then M becomes a new database owner.
Thus user substitution is a more general operation than database
ownership change.
Similarly as FBUsersSetup, DBUSubst.exe is written as a (harmless for
your computer) Inno Setup Windows installer. It basically is a wrapper for
the isql command line utility and
some sql scripts. The scripts are available in DBUSubst.zip.
They are documented and thus contain a detailed information about the
substitution process. The document DBUSubst.pdf
contains some introductory information about the user privileges and some Firebird internals.
Two essential dialog pages of DBUSubst.exe are
- the database connection
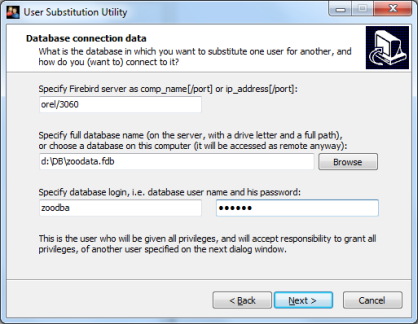
Our database zoodata.fdb resides on a computer orel where
(the relevant instance of) Firebird communicates thru port 3060;
orel can be a computer in the local network or a
computer visible on internet. Of course, if it is not the local computer
on which DBUSubst is run, the browse button cannot be used; the path to zoodata.fdb
has to be typed.
When developing the database, we accessed it as a user LION.
This user is an owner of the database.
We also have another user VISITOR who is designed to have some restricted
access. Now when the database is about to be
deployed, it appears that the name LION was not wisely selected and that the
owner name should be ZOODBA. So we are about to substitute ZOODBA for LION.
ZOODBA already exists on the server in question, i.e. orel/3060.
with the NEW user's login, and then
- the login of
the dead
user
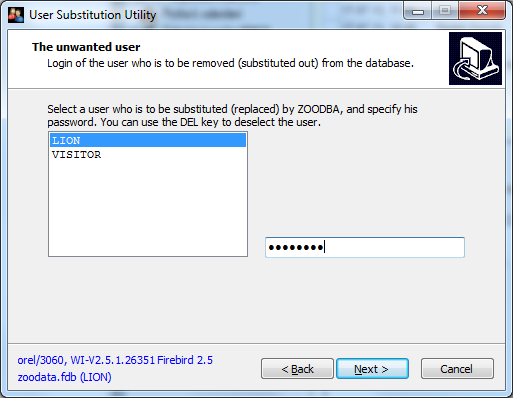
Since we were allowed to proceed to this dialog window, the login of
ZOODBA was verified against Firebird on orel/3060. It was also detected
that the version of this Firebird server is 2.5.1 and that the owner
of the database is LION, see the blue text labels in the bottom.
We are now selecting LION as the user who will be substituted by ZOODBA,
and we have to specify his password. The password of VISITOR is immaterial
for the current substitution process since VISITOR is not
a grantor of anything. However, if there were other users who
granted something to LION, further dialog windows asking about their
passwords would follow.
, i.e. the user who is to disappear.





